2024. 10. 11. 00:55ㆍR분석
단순회귀분석 코드연구
단순 회귀분석 코드연구 1
예측 모델링 설계목적 : diamonds데이터에서 가격별 무게의 상관관계를 알아보고 가격의 변동에 따른 무게예측하기
사용 데이터 : diamonds(r내장데이터)
#데이터 셋 로드
diamonds
#상관관계분석
cor.test(diamonds$price,diamonds$carat)
#p-value = < 2.2e-16
#cor= 0.9215913
#상관성 확인
#그래프로 상관관계확인
plot(diamonds$price,diamonds$carat)회귀분석 코드연구 1 다이아몬드 데이터의 무게와 가격의 상관관계를단하 분석한 결과이다. p-value가 < 2.2e-16이고 cor가 0.9215913으로 상관성이 확인되었으며

내장그래프인 plot을 사용하여 상관성을 확인하였을때도 어느정도 한 방향으로 관측점들이 분포하고있어, 상관성이 있다고 판단되었다.
#기울기, 절편 구하기
model<- lm(diamonds$carat~diamonds$price)
model
#기울기 절편 추출하기
b <- coef(model)[1]
w <- coef(model)[2]
b #종속변수가 0일때 y절편의 값(상수)
w #기울기
lm함수를 이용하여 기울기와 절편을 구했고, coef함수를 이용하여 기울기와 절편을 추출했다. 회귀모델을 평가할때 사용자 정의함수를 정의하여 평가할 예정이라 변수의 이름을 직설적으로 b와 w로 정의하여 변수에 저장했다.
#회귀모델 평가
#함수 생성
model_p <- function(x){
return(w*x+b)
}
model_p(20.1)
#예측값 저장
pred <- model_p(diamonds$carat)
pred
1차 회귀식을 그대로 사용자 정의함수로 정의했으며, 실제값 독립변수를 인수로 전달했을때 예측값이 나올수 있도록 return값을 정의했다. 함수를 생성하고 나서 함수작동이 되는지 확인을 위해 생성된 model_p함수에 값을 입력했을때 값이 나오는지확인후, 독립변수를 인수로 전달하여 예측값을 도출했고, 예측값과 실제값비교를 위해 변수에 예측값을 저장했다.
#예측값, 실제값, 오차 출력
dia_model <- data.frame(pred,diamonds$carat,abs(pred-diamonds$carat))
colnames(dia_model) <- c('예측값','실제값','오차')
View(dia_model)
예측값과 실제값, 그리고 예측값에서 실제값을 뺀 절대오차를 도출하여 한눈에 비교하기위해 데이터프래임에 지정한 후, 보다 좋은 가독성을 위해 View함수를 이용하여 표로 도출한 결과이다. 결과를 보면 오차범위가 0.05로 작은 수치도 있지만 0.15로 큰 수치를 보이는 데이터도 존재한다. 이런경우는 모델링 전체가 잘못됐다기보다는 특정 데이터에서만 모델이 예측을잘 하지 못하고 있다고 판단된다.
단순 회귀분석 코드연구 2
예측 모델링 설계목적 : mpg데이터의 displ에 따른 cty값 예측하기
사용 데이터 : mpg(r내장데이터)
*1과 동일한 방법이므로 동일한 부분은 설명 생략*
#데이터 셋 불러오기
library(ggplot2)
mpg <- as.data.frame(ggplot2 :: mpg) # 패키지 :: 데이터 : 패키지에 저장된 특정 데이터를 불러올 때 사용
mpg
#1) cty와 displ 두변수의 상관관계 계산
plot(mpg$cty,mpg$displ)
cor.test(mpg$cty,mpg$displ)
#p-value : < 2.2e-16
#cor : -0.798524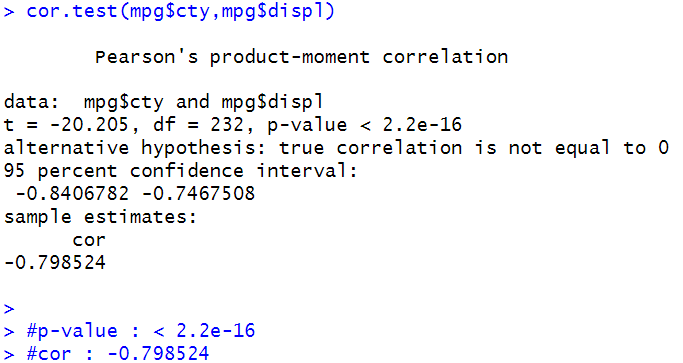
회귀분석에 사용할 데이터 셋을 준비해준 후에, displ와 cty의 상관관계를 cor.test함수를 이용하여 상관관계를 분석한다. 두 변수의 p-value가 < 2.2e-16 이고 cor 가 -0.798524로 음의 상관관계를 보여주고있음을 알 수 있다.
#2) displ(배기량)으로 cty(도시에서 연비)을 예측하는 회귀모델 생성
#모델 생성(절편, 기울기 구하기)
model <- lm(mpg$cty~mpg$displ)
model
#모델에서 절편과 기울기값 추출
b <- coef(model)[1] #절편(상수)
w <- coef(model)[2] #기울기#3) displ(배기량)데이터로 회귀모델을 적용하여
#cty(연비)에측값 계산
#사용자 함수 이용하여 풀기
#예측값 함수 정의
pred <- function(x){
return(abs(w*x+b))
}
pred<- round(pred(mpg$displ),0)
pred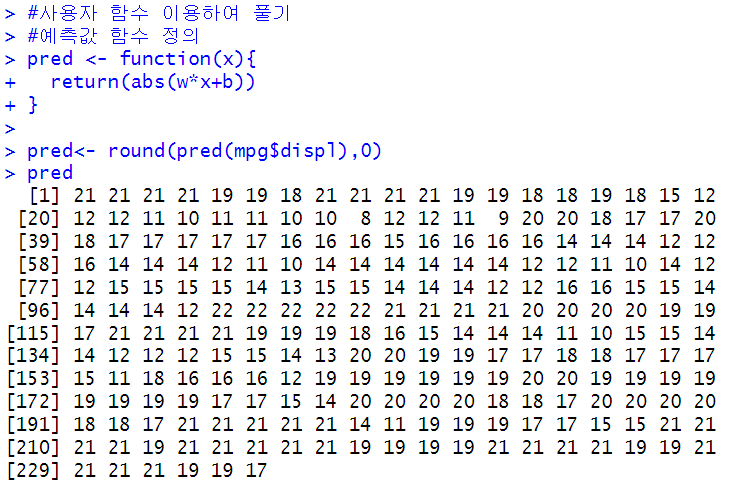
#실제값과 예측값 비교 및 오차범위확인
result <- data.frame(pred,mpg$cty,pred-mpg$cty)
colnames(result) <- c('연비 예측값','연비 실제값','오차범위')
View(result)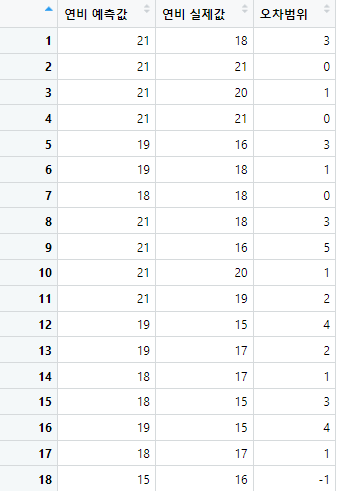
연비 예측값과 실제값, 그리고 절대오차를 구하여 데이터프레임으로 정리했다. 전반적으로 오차범위가 5이내를 머물고 있어, 안정적으로 예측이 되고있음을알 수 있다.
#모델의 성능 확인 (MAE)
MAE <- sum(abs(pred-mpg$cty))/nrow(mpg)
MAE #1.811966
range(mpg$cty) #9 35
이번 단순회귀분석에서는 모델성능을 좀더 정확하게 확인하기 위해 MAE값을 계산해보기로했다. MAE값은 예측값에서 실제값을 뺀 후 데이터의 수로 나눠주면 되며, 낮을 수록 좋은 성과라는 뜻이다. 모델의 MAE가 약 1.8정도를 보이고있는데 데이터의 범위가 9~35인것을 보면 현재 모델의 오차는 전체범위에서 약 6.95%정도에 해당한다고 할 수 있다. 이는 성능이 매우 우수하다고는 하기에는 어려우나, 꽤 양호한 수준의 오차범위를 보여주고있기때문에, 성능이 좋은 모델이 되었다고 볼 수 있다.
#예측된 값의 산점도 그래프 및 회귀선 그리기
mpg1 <- data.frame(
displ=mpg$displ,
cty=result$`연비 예측값`
)
mpg1
ggplot(mpg1,aes(x=displ,y=cty))+
geom_point(color='red')+
geom_abline(intercept=b,slope=w)+
labs(title='예측cty와 실제 displ의 상관관계')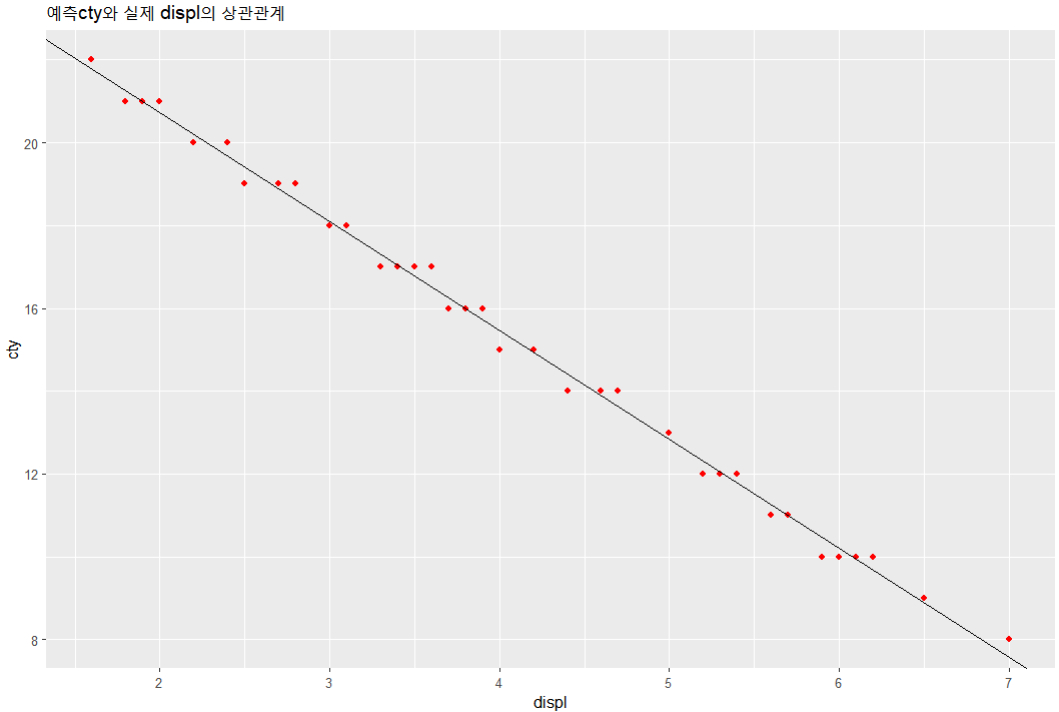
이번에는 예측값으로 산점도그래프를 그려, 상관관계가 있는지없는지까지 살펴보았다. 먼저, 종속변수는 예측된 값으로, 독립변수는 실제값으로 이뤄진 데이터프레임으로 데이터 셋을 준비하고 geom_point와 geom_abline을 이용하여 회귀선을 확인해보았는데, 굉장히 높은 음의 상관성을 보여주고있는 모습을 확인할 수 있었다.
같은 회귀분석 predict함수 이용하여 예측하기
#(predict함수사용해서 예측모델만들기)
#데이터 셋 불러오기
library(ggplot2)
mpg <- as.data.frame(ggplot2 :: mpg) # 패키지 :: 데이터 : 패키지에 저장된 특정 데이터를 불러올 때 사용
mpg
#1) cty와 displ 두변수의 상관관계 계산
plot(mpg$cty,mpg$displ)
cor.test(mpg$cty,mpg$displ)
#p-value : < 2.2e-16
#cor : -0.798524
#2) displ(배기량)으로 cty(도시에서 연비)을 예측하는 회귀모델 생성
#모델 생성(절편, 기울기 구하기)
model <- lm(mpg$cty~mpg$displ)
model
#모델에서 절편과 기울기값 추출
b <- coef(model)[1] #절편(상수)
w <- coef(model)[2] #기울기
#predict(모델,데이터 셋)함수 이용하여 풀기
pred <- predict(model,mpg)
pred #실수 출력. 형변환 필요
pred <- round(pred,0)
pred
#실제값 확인
mpg$cty
#정확도 확인
mean(pred==mpg$cty) #0.1752137
#모델의 성능 확인 (MAE)
MAE <- sum(abs(pred-mpg$cty))/nrow(mpg)
MAE #1.811966
다중 회귀분석 코드연구
예측 모델링 설계목적 : Sepal.Length, Sepal.Width, Petal.Length데이터를 가지고 Petal.Width의 값 예측하기
사용 데이터 : iris(r의 내장데이터)
#1)데이터셋 준비
iris
iris1 <- data.frame(
Sepal.Length=iris$Sepal.Length,
Sepal.Width=iris$Sepal.Width,
Petal.Length=iris$Petal.Length,
Petal.Width=iris$Petal.Width
)
iris1#필요한 데이터만 로드
#2)종속변수와 독립변수간의 상관성 확인
#패키지 로드
library(car)
library(GGally)
ggpairs(iris1,title='종속변수와 독립변수간의 상관성 확인')+
theme_minimal()
#Sepal.Length와Petal.Length 가장 높은 상관성을 보임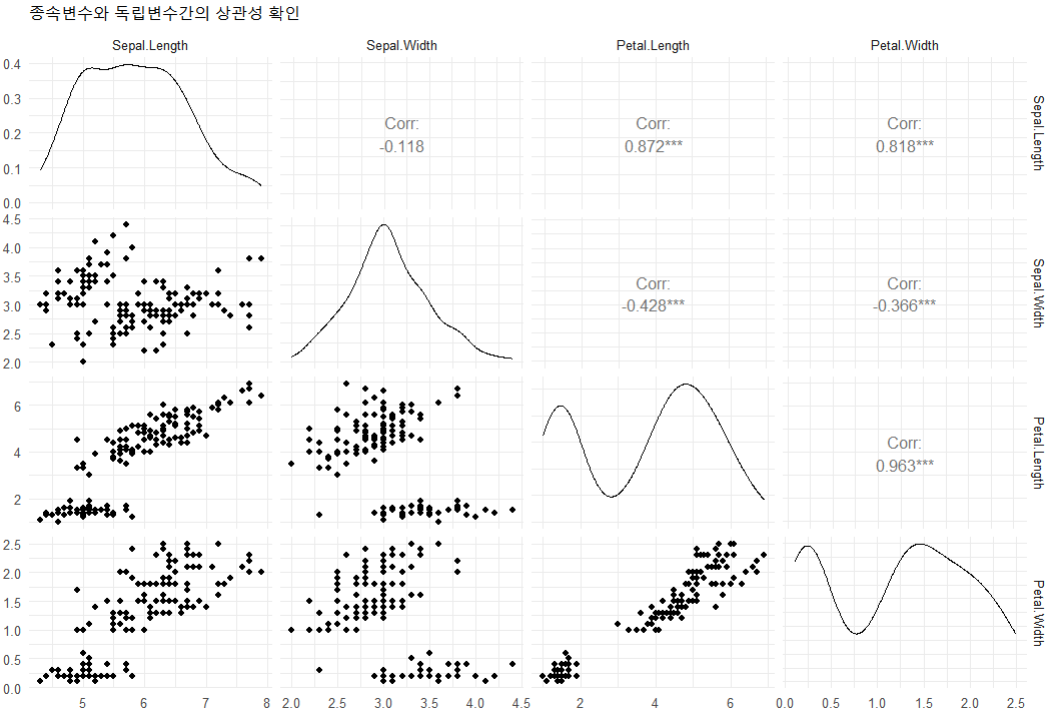
먼저 iris데이터를 다중회귀분석에 필요한 데이터들로만 구성하여 데이터셋을 준비한 후, 상관분석을 진행했다. 그전에 다중회귀분석에서 사용하는 car패키지와 GGally패캐지를 로드해주었다. 다중회귀분석에서는 산점도, cor까지 전부 한번에 확인할 수 있는GGally의 ggpairs함수를 사용했기때문에 따로 cor.test분석은 진행하지 않았다. 결과를 보면 Sepal.Length가 0.8,Petal.Length가 0.9로 가장 높은 상관성을 보이고 있음을 알 수 있다.
#3)절편,기울기 구하기 / 모델링
model <- lm(Petal.Width~Sepal.Length+Sepal.Width+Petal.Length,data=iris1)
model
summary(model)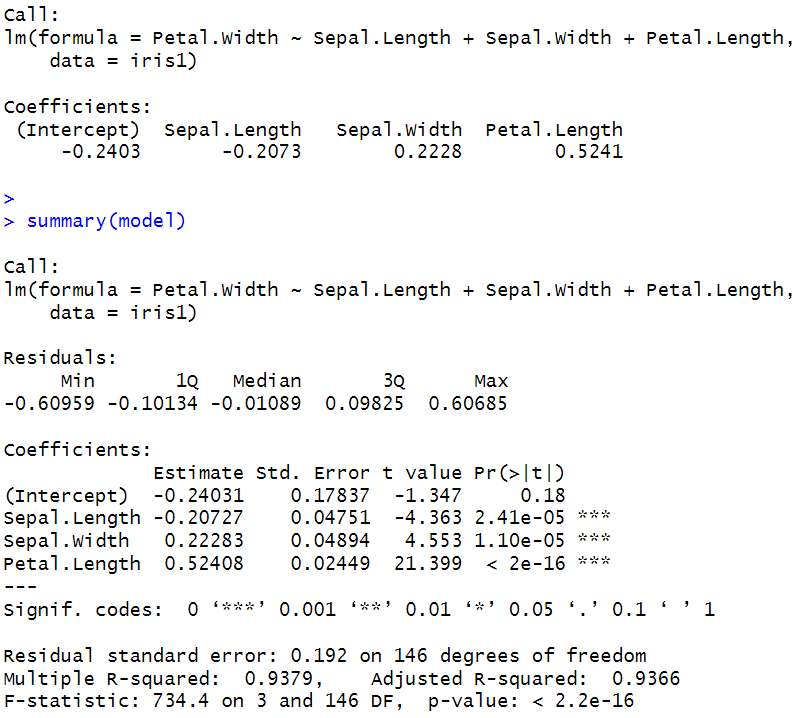
단순회귀분석과 동일한 방법으로 lm함수를 이용하여 가울기와 절편값을 구해주는데, 이때 다중회귀분석은 독립변수들이 많으므로 독립변수들을 +로 엮여 함수에 전달해야한다. 이렇게 모델링이 됐다면 생성된 모델을 summary함수를 이용하여 p-value값,***표시,Adjusted R-squared(결정계수)값을 확인해야하는데 p-value 가 < 2.2e-16이고 ***인 변수들은 Sepal.Length, Sepal.Width, Petal.Length이고, Adjusted R-squared는 0.9366이므로 이 모델링의 설명력이 약93.66%로 높은 설명력을 보이고 있다고 할 수 있다.
#4)다중 회귀분석 stepAIC진행
library(MASS)
model2 <- stepAIC(model)
model2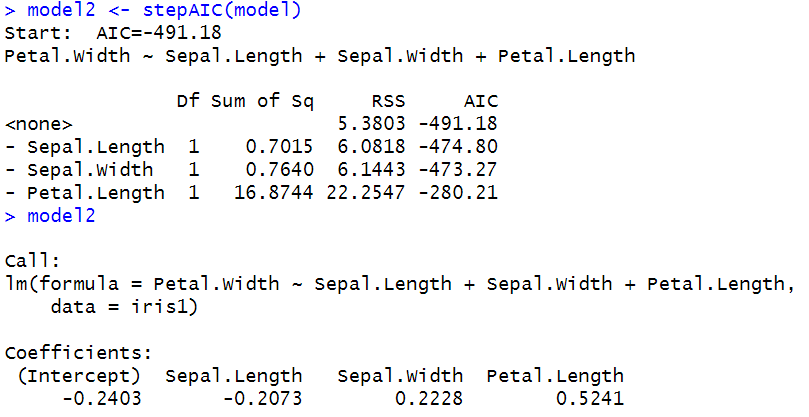
모델링이 끝났다면 패키지 MASS를 로드해준 후, stepAIC함수를 이용하여 다중회귀분석 모델링을 좀더 최적화하는 작업을 거쳐야한다. stepAIC는 스텝이 한번씩 진해될 수록 변수를 제거하거나 추가하면서 AIC값을 줄여나가는 과정을 거친다. 최종결과를 보면Sepal.Length , Sepal.Width, Petal.Length의 변수가 최종적으로 남게됐고, 그에따른 절편과 기울기가 함께 다시 도출된것을 확인할 수 있다. stepAIC를 하기전과 크게 변동사항이 없었기때문에 이미 그전의변수들의 선택이 최적의 선택이었던것을 알 수 있다.
#5)예측값 계산
#stepAIC를 통해 선택된 변수들로 생성된 새로운 model2사용
pred <- predict(model2,iris1)
pred <- round(pred,1)
pred
#6)예측값과 실제값 비교
result1 <- data.frame(pred,iris$Petal.Width,pred-iris$Petal.Width)
colnames(result1) <- c('예측값','실제값','오차범위')
result1
View(result1)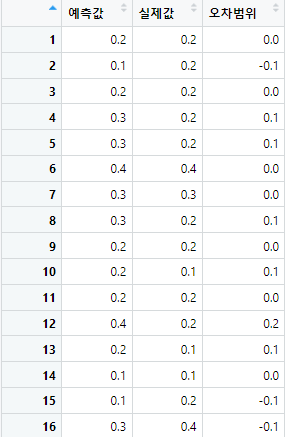
도출된 예측값을 출력하여 변수에 저장하고, 예측값과 실제값 비교를위해 데이터프레임으로 정리하여 저장해준 결과이다. 예측값과 실제값의 오차범위가 전반적으로 매우 좁게 나타나고있다.
#7)정확도 비교
mean(iris$Petal.Width==pred) #0.26
#하지만 Petal.Width의 경우 연속적인 값이기때문에
#관계연산자를 사용한 비교의 비율값은 올바르지 않을 수 있음
보다 자세한 결과를 보기위해 MAE값을 계산해보았다. 결과는 0.26으로 매우 낮은 값을 보이고있으나, 사용한 데이터의 값인 Petal.Width가 연속적인 숫자의 형식이기때문에 이런경우 MAE의값으로 본 비율의 값이 올바르지 않을 수도 있다. 하지만 이미 전반적으로 오차범위가 매우 좁고, 오차범위가 0.6이상을벗어나는 값이 없으므로 꽤 높은 예측률을 보여주는 모델이라고 할 수 있다.
로지스틱 회귀분석 코드연구
예측 모델링 설계목적 : mtcars데이터에서 mpg(연비),hp(마력),cyl(실린더 수)로 am(자동차 변속기 여부)예측하기
사용 데이터 : mtcars (r의 내장데이터)
#mtcars데이터에서 mpg(연비),hp(마력),cyl(실린더 수)로 am(자동차 변속기 여부)예측하기
#1)데이터 셋 준비
mtcars
data <- data.frame(
mpg = mtcars$mpg,
cyl = mtcars$cyl,
hp = mtcars$hp,
am = mtcars$am
)
data #am데이터가 이진분류인 범주형데이터 형태
#만약 문자형이라면 as.integer로 변환한 후 사용할것먼저 로지스틱 회귀분석에 사용할 데이터들을 준비해준다. 로지스틱회귀분석은 이진분류이거나 수치가 아닌 범주형데이터일때 정수형으로 형변환을 하여 진행하는 회귀분석이다. 지금 사용할 데이터는 문자형 범주형데이터가 아닌 이진분류로 되어있는 범주형데이터이므로 형변환은 따로 진행하지 않았다.
#2)절편,기울기 구하기 / 모델링
#로지스틱 회귀분석은 glm사용
model <- glm(am~.,data=data)
model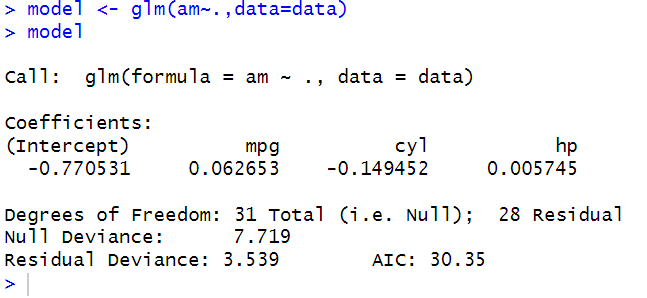
데이터 준비가 모두완료되었으면 기울기와 절편을 구해 모델링을 해주면되는데, 로지스틱회귀분석의 경우 lm이 아닌 glm을 사용하여 절편과 기울기를 구해준다.
#3)예측값 구하기
#실제 데이터 준비
real_am <-data.frame(
mpg = mtcars$mpg,
cyl = mtcars$cyl,
hp = mtcars$hp
)
real_am #am 값이 빠진 실제 데이터
pred <- predict(model,real_am)
pred
pred <- round(pred,0)
pred모델링 작업이 끝났다면 모델을 가지고 predict함수를 이용하여 예측값을 도출해준다. 예측값은 항상 실수형으로 출력되는데 실제값이 0과 1인 이진분류로 되어있기때문에 round함수를 함꼐 이용하여 예측값을 다시 저장해주었다.
#4)예측값과 실제값 비교
#실제값 데이터 준비
real_am <- data.frame(
am=mtcars$am
)
real_am
mean(real_am==pred) #0.84375
pred_data <- data.frame(pred,mtcars$am,pred-mtcars$am)
colnames(pred_data) <- c('실제값','예측값','오차범위')
pred_data
View(pred_data)
#정확도 계산
MAE <- sum(abs(pred-real_am))/nrow(data)
MAE #0.15625
sum(pred==real_am) #32개 데이터중 27개완벽 일치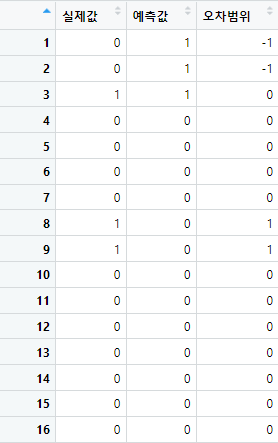

로지스틱 회귀분석도 마찬가지로 실제값, 예측값, 오차범위를 데이터프레임에 저장하여 정리했다. 전반적으로 오차범위가 0인데이터들이 대부분이며 MAE역시 약 0.15정도로 낮지만 애초에 값의 범위가 0~1로 이루어진 데이터이기때문에 보다확실하고 구체적인 모델성능 측정을 위해 관계연산자를 활용하여 총 몇개의 데이터가 완벽하게 일치하는지 알아보았다. 총 데이터32개중 27개의 데이터가 완벽일치했다. 과반수가 훨씬 넘는 수가 일치했기떄문에 꽤 성능이 좋은 모델이 구축되었다고 할 수 있다.
'R분석' 카테고리의 다른 글
| R복습_회귀분석 (1차 단순회귀분석, 다중회귀분석, 로지스틱 회귀분석) (1) | 2024.10.10 |
|---|---|
| R복습_데이터 시각화2_ (그래프에 회귀선그리기(단순회귀분석), 그래프 객체 추가,도형 및 화살표 추가) (0) | 2024.10.07 |
| R복습_데이터 시각화1_ ggplot2(산점도, 꺾은선, 막대, 누적,박스,히스토그램, 선버스트,gridExtra 등) (1) | 2024.10.07 |
| R복습_reshape2패키지와 함수(melt,cast,데이터구조 가공) (1) | 2024.10.06 |
| R복습_stringr패키지와 함수(문자열 가공) (0) | 2024.10.05 |